LOS NÚMEROS RACIONALES
Los números racionales son los que se pueden
representar por medio de fracciones. Representan partes de algo que se ha
dividido en partes iguales. Por ejemplo, si cortamos una naranja en 4 trozos
iguales y tomamos tres trozos de esta, nos hemos comido 3/4 de la naranja.
Un número racional es también, todo número
que puede representarse como el cociente de
dos enteros con denominador distinto de cero (una fracción común).
Los números racionales se representan con la letra Q
Decimos que a es un número racional,
si es posible expresarlo de la forma a=p/q, donde p, q Є Z y q ≠ 0.
De esta forma
De esta forma
Donde, p
es llamado numerador y q es el denominador de la fracción.
El conjunto de los racionales es denso porque entre dos números racionales siempre podemos encontrar otro número racional.
El conjunto de los racionales es denso porque entre dos números racionales siempre podemos encontrar otro número racional.
Son ejemplos de números racionales:
|
|
También son números racionales los números enteros:
- Los números
enteros se pueden expresar como fracción con denominador 1, por lo tanto, todo
número entero es también un número racional:
8=8/1 0=0/1 -5=(-5)/1 1=1/1 1=7/7
Un mismo número racional se puede expresar con varias fracciones. Por
ejemplo: 1/2
se puede expresar como: 2/4 , 3/6
De todas estas formas, la primera se llama fracción irreducible y las demás fracciones equivalentes.
Generalmente, los resultados fraccionarios
de diferentes problemas se deben expresar con el denominador en forma natural
(entero positivo distinto de cero).
Los números racionales son infinitos.
Aunque parezca increíble podemos asociar un número natural a cada número
racional. Muchas veces los números racionales se expresan como números
decimales. Por ejemplo:
1/2=0,5
3/4=0,75
Se pueden clasificar en dos grupos: Limitados y periódicos.
Estos últimos se pueden clasificar a su vez, en periódicos puros y periódicos
mixtos.
- Limitados: son
los que en su representación decimal tienen un número fijo de números. Por
ejemplo:
- Periódicos: son los que en su representación decimal tienen un número
ilimitado de números. Hay dos tipos de números periódicos:
- Los puros: cuando un número, o grupo
de números, se repite ilimitadamente, desde el primer decimal. (Por
ejemplo: 3.838383...).
- Los mixtos: un número o grupo de
números se repite ilimitadamente a partir del segundo o posterior decimal
(por ejemplo 3.27838383...).
Sea a/b
Є Q; se conviene en representar los números racionales preferentemente por
medio de fracciones en las cuales el denominador es un número entero positivo.
Recordemos además, que si aЄZ,bЄZ, b>0,el número racional a/b se puede considerar como el cociente que se obtiene al dividir a por b; en donde b indica el número de partes en que se divide la unidad y a el número de partes que se toman de esta división.
De esta manera, si se divide en dos partes iguales cada segmento unidad en la recta numérica, podemos representar los números racionales cuya representación fraccionaria tiene como denominador 2, como se muestra en el ejemplo siguiente.
Recordemos además, que si aЄZ,bЄZ, b>0,el número racional a/b se puede considerar como el cociente que se obtiene al dividir a por b; en donde b indica el número de partes en que se divide la unidad y a el número de partes que se toman de esta división.
De esta manera, si se divide en dos partes iguales cada segmento unidad en la recta numérica, podemos representar los números racionales cuya representación fraccionaria tiene como denominador 2, como se muestra en el ejemplo siguiente.
De igual
manera, si se divide en tres partes iguales cada segmento unidad en la recta,
podemos representar los números racionales cuya representación fraccionaria
tiene como denominador 3, como se muestra en el ejemplo siguiente.
SIMPLIFICACION DE
NUMEROS RACIONALES
Simplificar una fracción es transformarla en
una fracción equivalente más
simple.
Para simplificar una fracción dividimos numerador y denominador por
un mismo número.
Empezaremos
a simplificar probando
por los primeros números primos:
2, 3, 5, 7, ... Es decir, probamos a dividir numerador y
denominador entre 2 mientras
se pueda, después pasamos al 3 y
así sucesivamente.
Se
repite el proceso hasta que no haya más divisores comunes.
Si
los términos de la fracción terminan en ceros,
empezaremos quitando los ceros comunes finales del numerador
y denominador.
Si
el número por el que dividimos es el máximo común denominador del numerador
y denominador llegamos a una fracción irreducible.
m.c.d.(8, 36) = 4
llegar hasta la fracción irreductible, es decir, aquella fracción que no se
puede simplificar más (achicar más).
Ejemplos:
Amplificar
Es multiplicar el denominador y numerador de
una fracción por un mismo número. Este número permite que la
fracción aumente de valor tantas veces como veces se amplifica.
Por ejemplo, si la fracción se amplifica por dos, significa que
aumentará su valor al doble.
Siempre que se amplifique una fracción se obtendrán fracciones
equivalentes; es decir, fracciones que representan la misma cantidad.
Ejemplos:
Fracciones amplificadas por 3
(1×3)/(5×3)=3/15
(6×3)/(7×3)=18/21
ORDEN EN LOS NUMEROS RACIONALES
Cuando dos números racionales tienen el mismo denominador es mayor el
racional que tenga mayor numerador.
Ejemplo: 17/4 y 8/4 es mayor 17/4 porque tiene mayor el numerador.
Cuando los racionales tienen
diferentes denominadores necesario expresarlos como fracciones equivalentes, de
tal forma que tengan el mismo denominador. Luego se procede como cuando tienen
igual denominador.
Al representar dos números racionales en la recta numérica el racional que queda a la izquierda es menor
que el racional que queda a la derecha.
Observemos en la recta numérica que -5/2 es menor que -1/2.
EJERCICIOS PROPUESTOS
1.
11.Busca amplificando o
simplificando 10 fracciones equivalentes a 6/12
22.Represente en la
recta numérica los siguientes números racionales:
a) -5/6
b) 7/3 c)
9/4 d) -12/5
e) 14/9 f) -9/2
3.Establece la relación
menor que hay entre los siguientes racionales:
a) 5/2, 1/5 b) -5/2, 1/5 c) 8/5, 5/8 d) -8/5, -5/8
44. Representa en la
recta numérica -8/5 y -5/8 compara las posiciones que ocupan ¿cuál de los
racionales está a la izquierda? ¿cuál es menor?
55.Ordena de menor a
mayor los siguientes racionales :
a) 9/2, 3/8, 5/4 b)-7/3, 1/6, 5/2 c)
-3/4, -1/2, -3/10
6.Completa el dato o dibujo que falta para que la fracción se pueda leer
correctamente:
Nombre
|
Dibujo
|
Numerador
|
Denominador
|
Fracción
|
||||||||||||||
Tres octavos
|
3
|
8
|
|
|||||||||||||||
Cinco doceavos
|
||||||||||||||||||
7
|
10
|
|||||||||||||||||
Dos quintos
|
||||||||||||||||||
4
|
5
|
|||||||||||||||||
Un medio
|
||||||||||||||||||
2
|
3
|
|||||||||||||||||
Cuatro séptimos
|




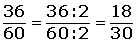





No hay comentarios:
Publicar un comentario