REGLA DE TRES
La regla de tres es
una forma de resolver problemas de proporcionalidad entre tres o más valores conocidos y una
incógnita. En ella se establece una relación de linealidad (Proporcionalidad) entre los valores involucrados.
Regla de
tres es la operación de hallar el cuarto término de una proporción conociendo
los otros tres.
La regla de tres más conocida es
la regla de tres simple directa, si bien resulta muy práctico conocer la regla
de tres simple inversa y la regla de tres compuesta, pues son de sencillo
manejo y pueden utilizarse para la resolución de problemas cotidianos de manera
efectiva.
REGLA DE TRES SIMPLE DIRECTA
Dadas dos magnitudes, se conocen la equivalencia entre un valor de una y el valor de la otra. Entonces para cada nuevo valor que se de a una magnitud calculamos el valor proporcional de la segunda magnitud
El precio de tres bolígrafos es de $ 4.5 ¿Cuánto cuestan 7 bolígrafos?
Ejemplo 1
En 50 litros de agua de mar hay 1300 gramos de sal.
¿Cuántos litros de agua de mar contendrán 5200 gramos de sal?
Como en doble cantidad de agua de mar habrá doble
cantidad de sal; en triple, triple, etc. Las magnitudes cantidad de
agua y cantidad de sal son directamente
proporcionales.
Si representamos por x el número de litros que
contendrá 5200 gramos de sal, y formamos la siguiente tabla:
|
Litros
de agua
|
50
|
x
|
|
Gramos
de sal
|
1300
|
5200
|
Y como en toda proporción el producto de medios es
igual al producto de extremos, resulta:
50.5200=1300.x
Es decir
En la práctica esto se suele disponer del siguiente
modo:
|
Esta
forma de plantear y resolver problemas sobre proporciones se conoce con el
nombre de regla de tres simple directa.
|
Ejemplo 2
Un coche gasta 5 litros de gasolina cada 100 km. Si
quedan en el depósito 6 litros, ¿cuántos kilómetros podrá recorrer el coche?

Luego con 6 litros el coche recorrerá 120 km
REGLA DE TRES SIMPLE INVERSA.
Dadas dos magnitudes, se conocen la equivalencia entre un valor de una y el valor de la otra. Entonces para cada nuevo valor que se de a una magnitud calculamos el valor proporcional inverso de la segunda magnitud
Ejemplo1
En una granja avícola hay 300 gallinas que se comen
un camión de grano en 20 días. Si se compran 100 gallinas más ¿En cuanto tiempo
comerán la misma cantidad de grano?
Ejemplo 2
Un ganadero tiene pienso suficiente para alimentar
220 vacas durante 45 días. ¿Cuántos días podrá alimentar con la misma cantidad
de pienso a 450 vacas?
|
Nº de
vacas
|
220
|
450
|
|
Nº de días
|
45
|
x
|
Vemos que con el mismo pienso, si el número de
vacas se duplica, tendrá para la mitad de días; a triple número de vacas,
tercera parte de días, etc. Por tanto son magnitudes inversamente
proporcionales.
x= número de días para el que tendrán comida las
450 vacas
|
Nº de
vacas
|
220
|
450
|
|
Nº de días
|
45
|
x
|
Se cumple que: 220.45=450.x, de donde
En la práctica esto se suele disponer del siguiente
modo:
Luego 450 vacas podrán comer 22 días
|
Esta
forma de plantear y resolver problemas sobre proporciones se conoce con el
nombre de regla de tres simple inversa.
|
REGLA DE
TRES COMPUESTA
La regla de tres compuesta se emplea cuando se
relacionan tres o más magnitudes, de modo que a partir de las
relaciones establecidas entre las magnitudes conocidas obtenemos la
desconocida.
Una regla de tres compuesta se compone de varias reglas
de tres simples aplicadas sucesivamente.
Como entre las magnitudes se pueden establecer relaciones de proporcionalidad
directa o inversa, podemos distinguir tres casos de regla
de tres compuesta:
REGLA
DE TRES COMPUESTA DIRECTA
Ejemplo
Nueve grifos
abiertos durante 10 horas diarias han consumido una cantidad de agua por valor
de 20 €. Averiguar el precio del vertido de 15 grifos abiertos 12 horas durante
los mismos días.
A más grifos, más euros
Directa.
A más horas, más euros
Directa.
9 grifos
10 horas
20 €
15 grifos
12 horas
x €
REGLA DE TRES COMPUESTA INVERSA

Ejemplo
5 obreros trabajando, trabajando 6 horas diarias construyen un muro en 2
días. ¿Cuánto tardarán 4 obreros trabajando 7 horas diarias?
A menos obreros, más días
Inversa.
A más horas, menos días
Inversa.
5 obreros
4
obreros
7 horas
x días
EJERCICIOS
PROPUESTOS
Regla de tres simple directa
1.100 litros de
aceite cuestan 189 €. ¿Cuánto cuestan 125 litros del mismo producto?
2. En un restaurante para
ubicar 18 mesas se necesitan 72 sillas.
Si hay 200 sillas, ¿Cuántas mesas más se pueden armar?
3.Una oveja atada a un poste con una soga de 4m,
demora 8 horas en comer el pasto a su alcance.
¿Cuánto demoraría en comer el pasto a su
alcance, si la soga midiese 2m?
4. El sacristán de una iglesia, da 16 campanadas en
8 segundos. ¿Cuántas campanadas dará en 48
segundos?
segundos?
5. Isabel escribe 3/5 de su reporte en 3.2 horas. A
la misma velocidad de escritura. ¿Cuántos minutos más necesitará para
terminar su reporte?
Regla de tres simple inversa
1. Un grupo de 5 personas consume una cantidad de gaseosa en 40
minutos. En cuanto tiempo consumirá la misma cantidad de gaseosa un grupo de 8
personas?
2. En un cuartel 200 soldados tienen comida para 40
días, si se cuadriplicara el número de soldados. ¿Cuánto tiempo les duraría la
comida?
3. Una obra puede ser realizada por 6 obreros en 20 días.
¿Cuántos obreros más se necesitarán para hacer el mismo trabajo en las
3/10 partes de ese tiempo?
4. Camila tiene 21 conejos y raciones de alimento
para 45 días. Como su amiga Paula le regala algunos conejos más, las raciones
le alcanzarán solo para 35 días. ¿Cuántos conejos le regaló Paula a Camila?
5. Un grupo de cinco cocineros iban a preparar un banquete en 6
horas. ¿Qué tiempo demoran 3 cocineros en preparar dicho banquete?
REGLA DE TRES COMPUESTA
1) Una familia compuesta de 6 personas consume en 2 días 3 kg de pan.
¿Cuántos kg de pan serán consumidos en 5 días, estando dos personas
ausentes?
2) 5 personas consumen 3 litros de jugo de naranja en 2 horas. ¿Cuántos
litros de jugo consumirán 20 personas durante 5 horas?
3)para preparar 30 emparedados utilizando 4 máquinas se emplearon 30
minutos. ¿Cuánto tiempo se empleara para hacer la misma cantidad de emparedados
utilizando 6 maquinas
4)ocho reflectores consumieron 60 vatios durante 4 horas. ¿Cuántos
vatios consumirán 12 reflectores durante 5 horas?

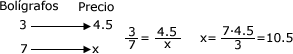

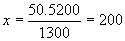




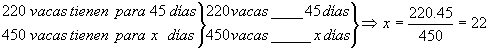



No hay comentarios:
Publicar un comentario